Quaternion 개념 정리-part1(복소수 기본개념)

오늘은 3D 게임 프로그래밍을 하다보면 자주 만나게되는 쿼터니온의 수학적 배경에 대해서 정리해 놓으려고 합니다. 참고문헌은 다음과 같습니다.

한정현. 게임 프로그래밍을 위한 3차원 그래픽스. 2011. 11장

TOMAS AKENINE-MOLLER. Real time rendering 3th edition. Chapter4

사원수는 회전과 방향을 나타낼 때 굉장히 매력적인 도구입니다. 축이랑 각도가 주어질 때 이걸 쿼터니언으로 바꾸는건 꽤나 쉬운 일이지만 만약 오일러 각으로 바꾸려한다면?? 으으 꽤나 복잡해집니다. 또한 오일러 회전 행렬과 함께할때는 보간과 짐벌락 문제까지 안고 있죠. 이번 포스팅을 통해 쿼터니언에 조금 더 가까워 질 수 있는 기회가 되었으면 좋겠습니다.

그럼 ㄱㄱ

복소수(Complex number)

방정식 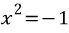이 실수해를 갖지 않는다는 문제를 해결하기 위해 18세기 수학자들은 가상의 허수 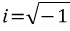를 만들었는데 이건 다음의 성질을 만족한다고 가정합니다.

.

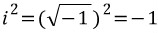그 외에는 실수의 대수적 성질을 따릅니다.
a, b가 실수일 때 a + bi or a + ib 이런 표현을 복소수(Complex Number)라고 부릅니다.
이 때 a를 Real part 부분, bi를 Imaginary part 라고 부릅니다.

또한 z0 = a + bi, z1 = c + di일 때 z0 = z1을 만족하려면 a = c, b = d이면 되고,
또한 z= a + bi에서 리얼 파트인 a= 0일 때 복소수 z = bi를 pure imaginary(순허수) 라고 부릅니다.
반대로 허수가 0인 복소수는 그냥 실수이므로 실수는 복소수의 부분집합이라고 볼 수 있습니다.

복소수의 덧셈 뺄셈 곱셈

​복소수는 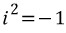로 두면 표준 대수 연산규칙에 따라 더하고 빼고 곱하고 할 수 있습니다.

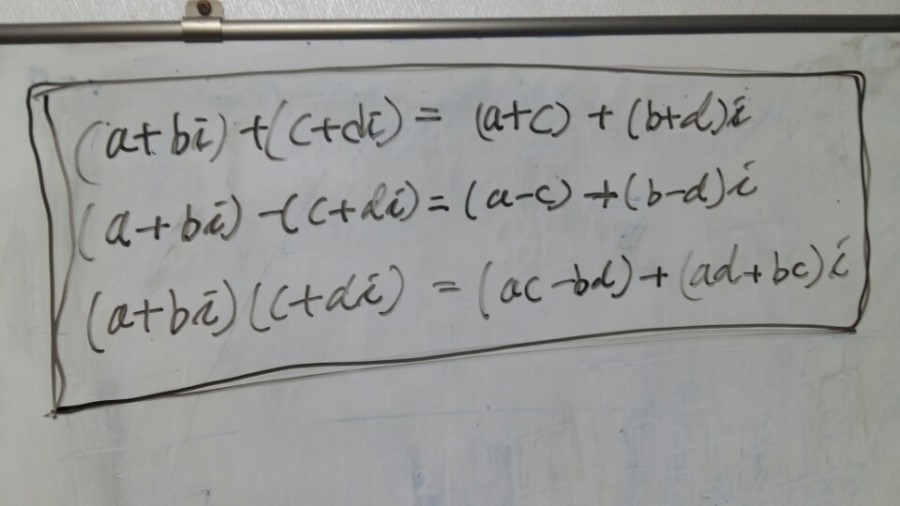
[그림 1]

복소평면

​복소수 z = a + bi는 실수의 순서쌍 (a,b)로 연관될 수 있습니다.
그말은 즉슨 그냥 2차원 평면상에 점이나 벡터로 나타내는 것이 가능합니다.
이것을 복소평면(Complex plain)이라고 부릅니다.

​ x축상의 점들은 허수가 0이니까 실수에 해당하고, y축상의 점들은 실수가 0인 Pure imaginary에 해당합니다. 따라서 x축을 Real axis, y축을 Imaginary axis로 부를 수 있습니다.

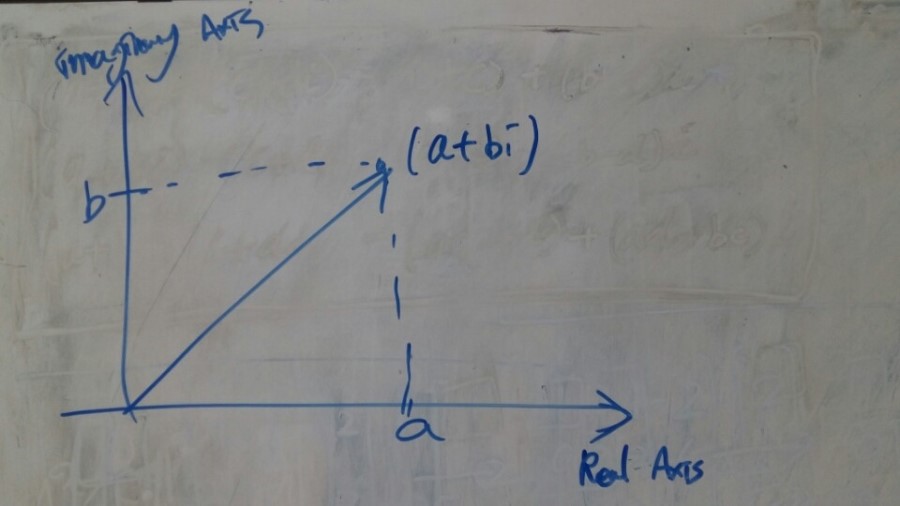
[그림 2]

복소켤례(complex conjugate)

​z = a + bi가 복소수일 떄 complex conjugate는 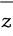( z bar라고 읽음) 로 표기하고 다음과 같이 정의합니다.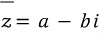

이는 단순히 허수부의 부호를 거꾸로 놓은 것이고, 기하적으로는 x축 기준으로 z를 반사시킨것에 불과합니다.

ex)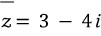

여기서 재미(?)난게 있는데요. 어떤 복소수와 복소켤례의 곱은 0이 아닌 실수라는 것입니다!!!

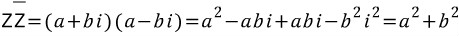
루트를 씌워주면 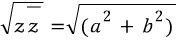이고, 이는 벡터의 길이입니다.

따라서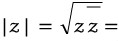 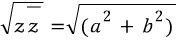이고, 이는 복소수의 크기가 됩니다!!

Inverse

z != 0일 때 inverse는 1/z 즉 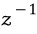입니다. 이건 1/z의 값은 분자 분모에 켤례 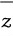를 곱하면 쉽게 계산 가능합니다.

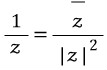
이번 포스팅은 여기까지입니다. 다음 포스팅에서는 본격적인 사원수에 관한 내용을 정리하도록 하겠습니다.