Quaternion 개념 정리-part2(사원수 배경지식)

이제 정신이 조금 돌아왔으므로 차분하게 다시 포스팅을 이어가겠습니다.

지난 시간에는 복소수의 기본 개념을 정리했습니다. 이번 시간에는 쿼터니온의 기본 개념을 정리할 예정입니다.

쿼터니온은 q는 복소수의 개념을 확장한 것으로 다음과 같이 네 항으로 표현합니다.

쿼터니온의 정의

[그림1]

그림에서와 같이 quaternion는 일종의 벡터로써 표현되며,
3개 부분은 허수부(imaginary part) 나머지 부분은 실수부(mistake part real part)라고 불립니다.

허수부는 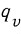와 같이 종종 줄여쓰므로 쿼터니온은 (Qv, Qw)와 같이 표현하기도 합니다.

이 때 허수부분에는 아주 중요한 특징이 있습니다. 두 개의 허수단위가 곱해지면 순환치환(Cycle permutation)의 특징을 갖습니다.

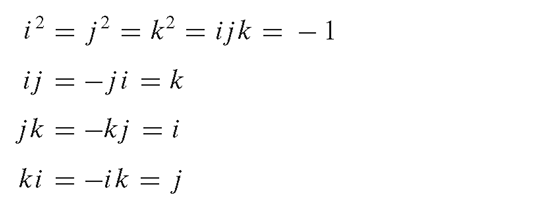
[그림2]

쿼터니온의 연산

또한 허수부에 대해서는 우리가 알고 있는 모든 벡터 연산을 적용할 수 있습니다. 예를 들면 덧셈, 비례, 닷프로덕트, 크로스 프로덕트.

만약 두 개의 사원수 q, r 이 있다고 가정하면 이들의 곱셈은 다음과 같이 표현할 수 있습니다.
이것은 [그림2]의 특징을 이용한 단순한 식의 전개입니다. 개인적으로 손으로 한 번 써보는 것을 추천합니다.

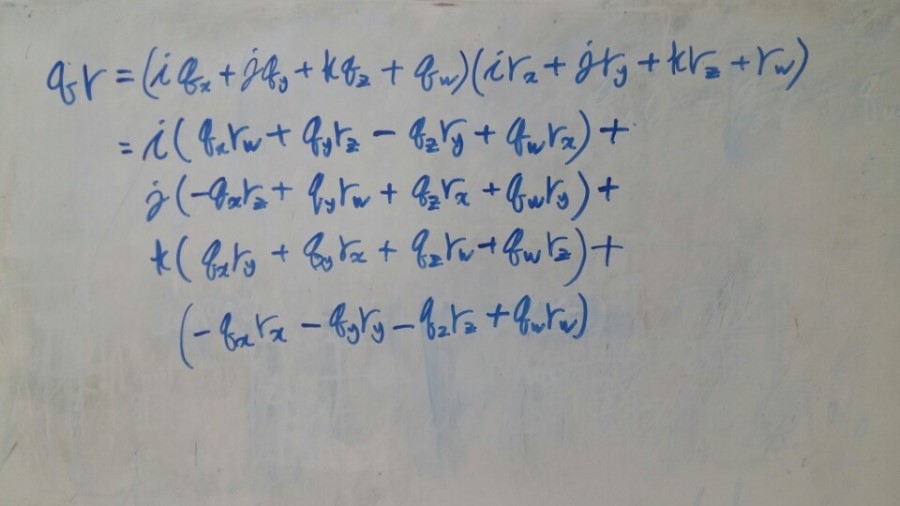
[그림3]

Conjugate(켤례) and Norm(쿼터니온의 크기) 그리고 Unit quaternion(단위 쿼터니온)

​일반 Complex number처럼 quaternion 도 conjugate를 갖습니다.
켤례는 복소수에서 모든 허수부분의 부호를 바꾸는 것이 정의였는데 ​쿼터니온도 마찬가지입니다.
그리고 쿼터니온의 Norm(쿼터니온의 크기) 역시 복소수와 마찬가지로 계산됩니다.

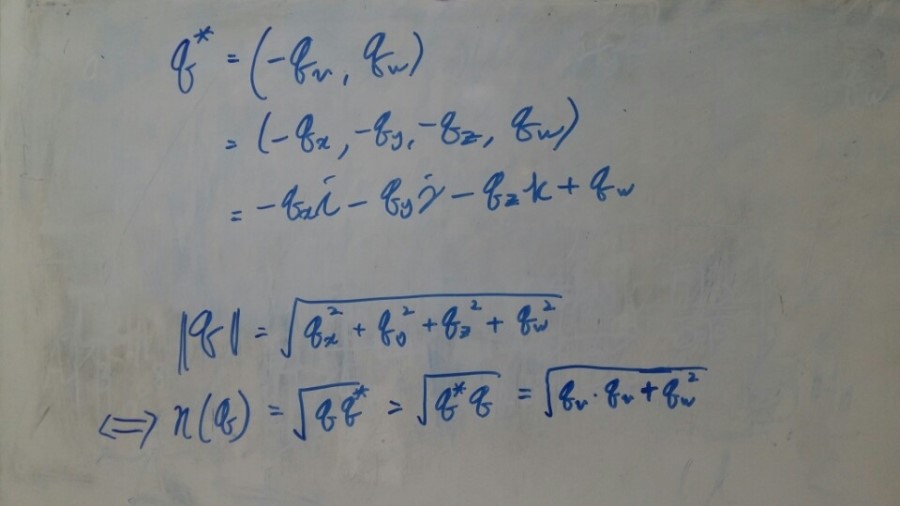[그림4]

만약에

q

= 1이라면 q는 단위 쿼터니온(unit quaternion)이라 불립니다.

Inverse 쿼터니온의 인버스 또한 복소수의 인버스와 같은 방식입니다.

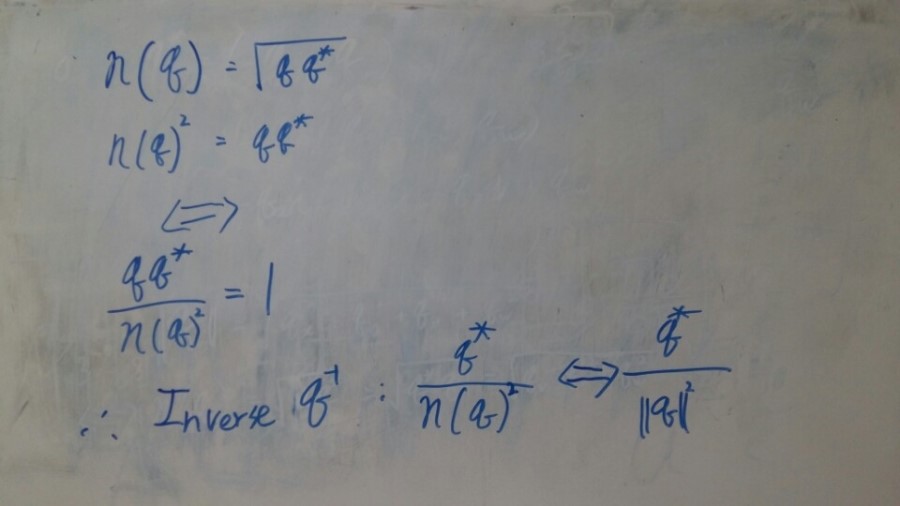[그림5]

규칙 모음

지금까지 쿼터니온의 Definition, operation, conjugate, norm, inverse의 정의들에 대해 살펴보았습니다. 다음은 위 정의로부터 나오는 주요 법칙들에 대해 나열해보겠습니다.

여기 단위 쿼터니온에서 이제 재밌는게 나오는데요.
그림9에서 n(Uq) = 1인 단위 쿼터니온은 이제 설명할 사원수 회전을 나타내는데 아주 적합한 친구입니다!_!

하지만 그 전에 오일러의 공식을 이해하고 넘어가면 쿼터니언을 직관적으로 이해하는데 조금 도움이 됩니다. 히힛 그래서 다음 포스트는 오일러의 공식을 e해 하고 가는 시간이 될 것 같습니다!

다음 포스트에서 만나요 !