Quaternion 개념 정리-part4(쿼터니언을 이용한 회전)

헬로우 안녕하세요. 이번 포스팅에서는 드디어 쿼터니언 회전에 대해 설명하겠습니다.

part1에서 복소수는 x값을 실수부로 y값을 허수부로 가지는 형태의 극좌표 표현이 가능하다고 했습니다.
그림으로 나타내면 다음과 같습니다.

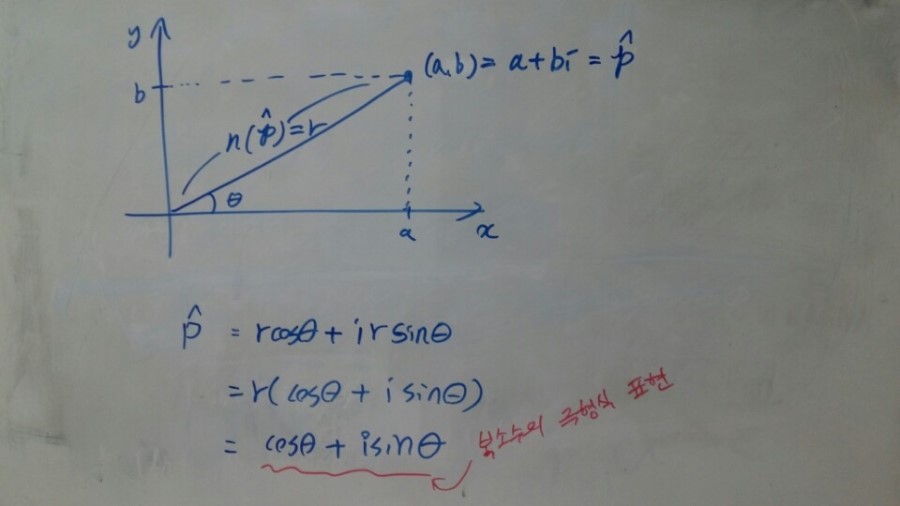
[그림1]

만약 복소수의 크기가 1이라고 할 때 복소수는 다음과 같이 오일러 공식의 형태가 나옵니다!! 자 그럼 이걸 ​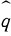 라고 하고 복소수의 일반형인 ​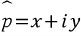와 곱해봅시다.

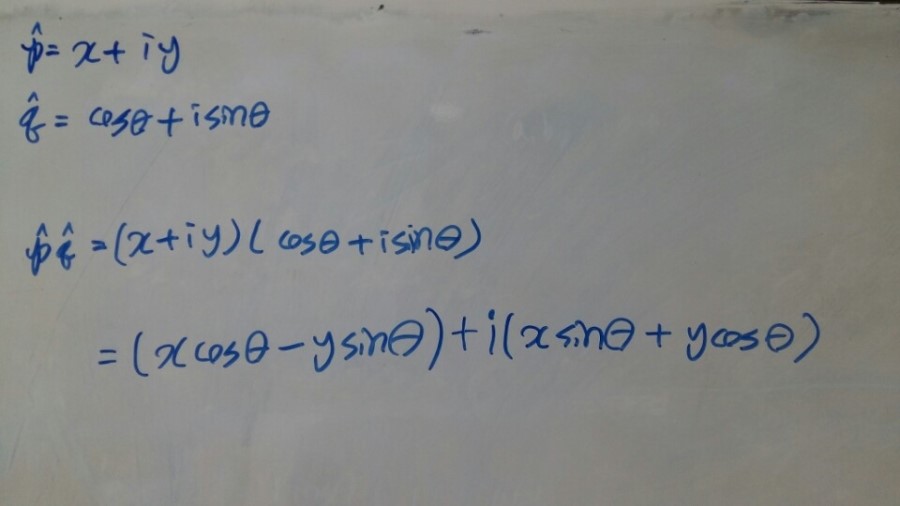
[그림2]

헉! 어디서 이 식을 많이 본 것 같지 않습니까? 그렇습니다. 2차원에서의 오일러 회전 행렬과 같은 모습이 됩니다!

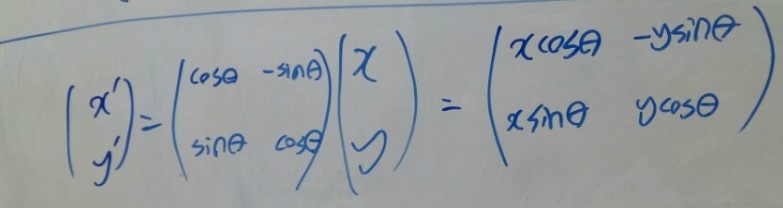
[그림3]

자! 여기서 우리는 어떤 복소수의 일반형 p = x + iy 에 복소수의 극좌표형 q = cos(theta) + isin(theta) 를 곱하면 그것이 p를 구성하는 벡터(x,y)의 회전을 의미한다는 것을 알게되었습니다.
그러면 이것을 3차원으로 확장시켜봅시다.
3차원에서의 쿼터니언 회전을 위해서 우선 회전할 벡터가 필요합니다.
하지만 이 회전할 벡터 자체는 쿼터니언으로 표현될 필요가 있는데 이 쿼터니언을 ​P ​로 표기하면

P = (Pv, Pw)
P = (p,0)

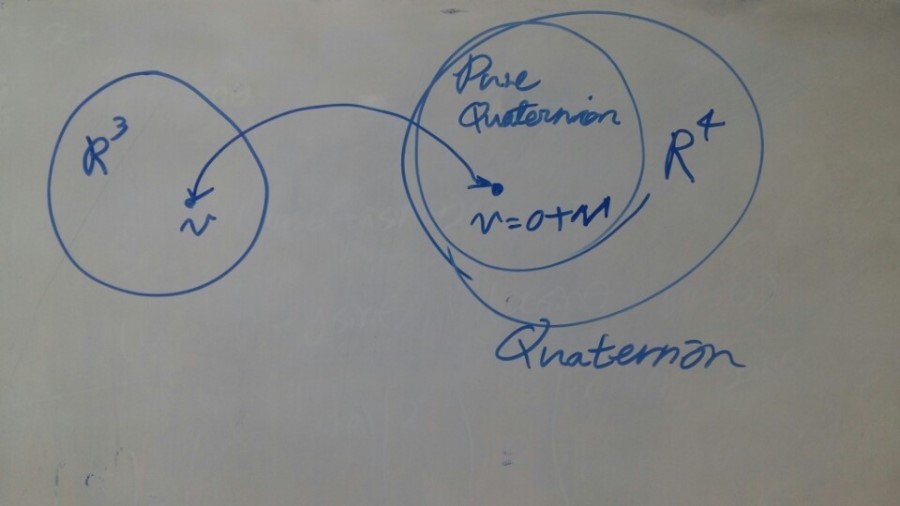
​실수부가 0, 허수부가 벡터p인 pure quaternion가 됩니다.
이 작업을 4차원 세상의 쿼터니언과 3차원 세상의 벡터가 소통 가능하게 만드는 과정이라고 생각하시면 됩니다.
이런 느낌

[그림4]

이제 회전하고 싶은 벡터가 생겼으니 회전축 u와 회전각 theta를 통해 회전 쿼터니언 q를 정의할 차례입니다.
이 때 회전 쿼터니언 q의 크기는 1인 unit quaternion이 되어야합니다.
그리고 이 유닛 쿼터니언은 극형식으로 나타내야합니다!

이전 part3에서 은근슬쩍 소개하고 넘어갔었는데 크기가 1인 쿼터니언은 극형식으로 다음과 같이 나타냅니다.

[그림5]

Norm을 계산해보면 Norm(q) = qq* = sin^2 + cos^2 = 1인 것을 확인할 수 있죠

자 그럼 이제 회전하고 싶은 벡터를 나타내는 쿼터니온 P = (Pv, 0),
그리고 회전 자체를 나타내는 쿼터니언 극형식 Q = UqSin(theta) + cos(theta) 를 정의했으니 이제 회전을 계산하는 일만 남았습니다.

Ken Shoemaker 형님의(신발파는사람아님) 쿼터니언 논문에 따르면,
P를 축 Uq를 중심으로 2theta만큼 회전하는 것은 다음과 같이 표현됩니다.

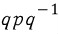
그런데 q는 unit quaternion이므로 다시 이렇게 표현 가능합니다. (part2 그림5 참고)

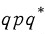
이 공식의 결과로 우리는 2theta 만큼 회전된 결과를 쿼터니언의 허수부 파트로부터 얻을 수 있습니다!
2theta가 아닌 theta만큼 회전한 결과를 얻고 싶다면 q를 만들때 theta/2를 사용하면 되겠죠

만약 연속해서 회전하고 싶다면 어떻게해야 할까요?
쿼터니언 회전 연산은 concatenation 합니다.
따라서 p를 q만큼 회전시키고 다음 r만큼 회전하는 경우 다음과 같이 표현 가능합니다.

[그림6]

야호! 이제 우리는 쿼터니언을 사용하여 벡터를 원하는 축에 대하여 간단하게 회전하는 것이 가능해졌습니다! Level up!

다음시간에는 Quaternion을 회전행렬로 변환하는 방법과 Spherical Linear Interpolation(구면선형보간)에 대해 설명하도록 하겠습니다.

part5에서 봐요