Quaternion 개념 정리-part5(쿼터니언의 행렬표현)
January 2, 2017
이번 시간에는 쿼터니언을 회전 행렬로 변환하는 방법에 대해서 알아보겠습니다.
쿼터니언 회전 연산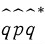 
는 단순 쿼터니온의 곱셈으로 이루어져 있고 쿼터니온의 곱셈은 단순한 식의 전개에 불과하므로 행렬로 나타낼 수 있습니다.
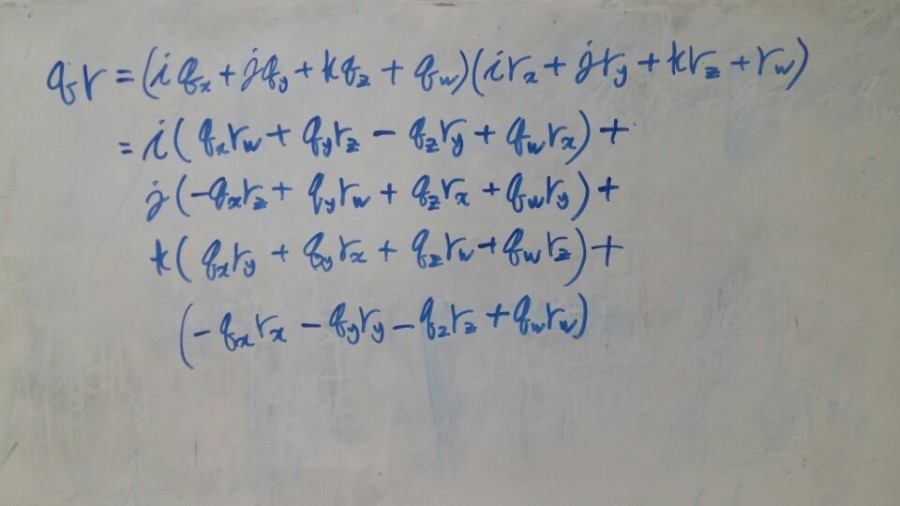
[그림1]
우선 qpq*를 설명하기 위한 예제로 두 쿼터니온의 곱셈 pq를 행렬로 표현해보면
다음의 두 가지 형태로 표현 가능합니다.
[그림2]
그럼 이 형태를 기반으로 qpq*에 대해 생각해보면 다음과 같이 정리됩니다.
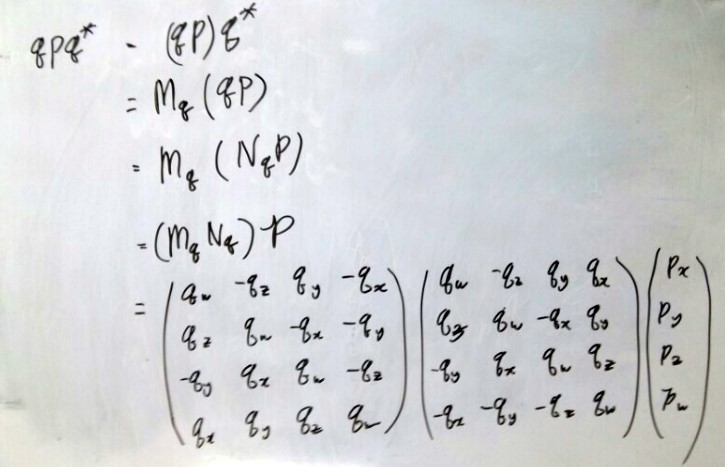
[그림3]
이제 Mq Nq부분을 계산하여 정리하면
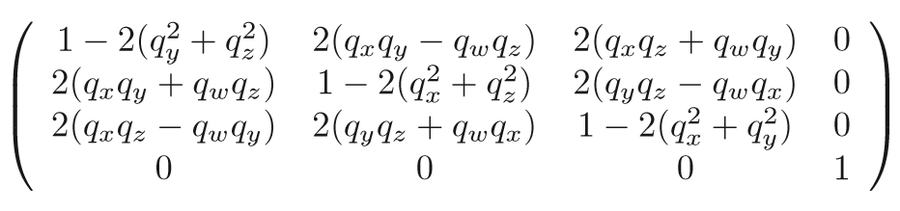
[그림4]
짠. 매트릭스 완성! 이걸 Mq라고 부르겠습니다.
이제 우리는 쿼터니언의 회전을 행렬의 형태로 표현하는 것이 가능해졌습니다!
자 그럼 반대는 어떻게할까요?
핵심은 이 행렬의 다음 특징에 있습니다.
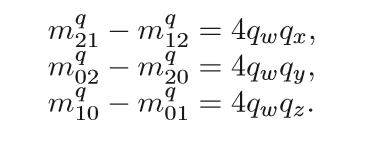
[그림5]
만약 쿼터니언의 실수 파트인 Qw만 알고 있다면 나머지 Qx, Qy, Qz를 알아내는 것이 가능해집니다.
자 그럼 Qw를 어떻게 알아내는지 본 후에, Qx, Qy, Qz를 자연스럽게 알아내 봅시다!
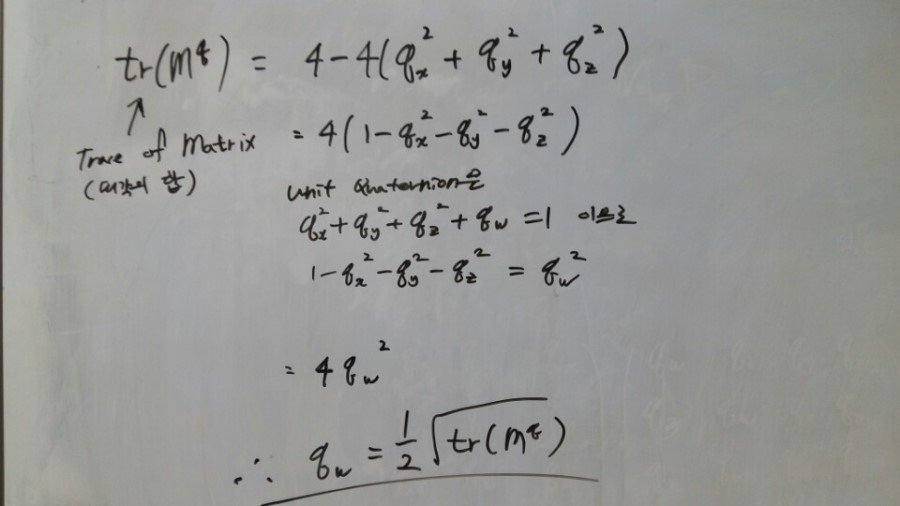
[그림6]
어때요 간단하게 Qw를 알아냈죠? Qx, Qy, Qz는 Qw로 부터 알아낼 수 있으므로 정리하면
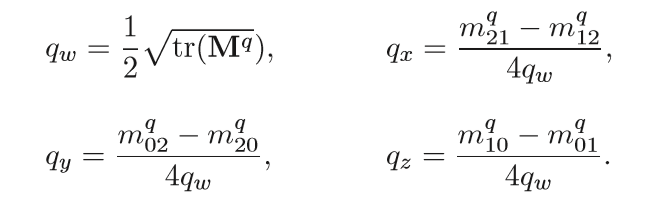
[그림7]
이렇게 됩니다!
자 이제 우린 행렬을 쿼터니온으로 쿼터니온을 행렬로 만드는 것이 가능해졌습니다!
참 쉽죠?
추가내용
Qw가 0 또는 0에 매우 가까운 경우 qx, qy, qz를 구하는 식은 문제가 될 수 있는데 관련 내용 해결을 위한 추가설명과 링크입니다.
0또는 매우 작은수 나누기 문제를 피하기 위한 방법이 있습니다.
Qx, Qy, Qz, Qz로 구성된 매개변수 t를 다음과 같이 설정하면 이런 식을 만들 수 있습니다.
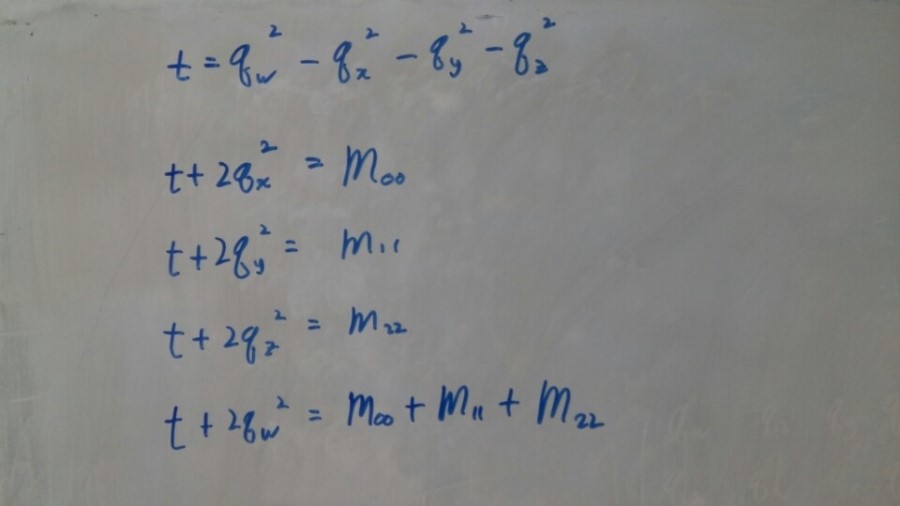
[그림8]
그러면 행렬의 대각성분들만 이용해서 Qx, Qy, Qz, Qw간의 크기를 비교하는게 가능해지는데요
크기비교를 했을때 Qw가 가장 크다면 기존의 식을 적용하면 되고,
만약 그렇지 않은 경우에는 다음 식을 이용합니다.
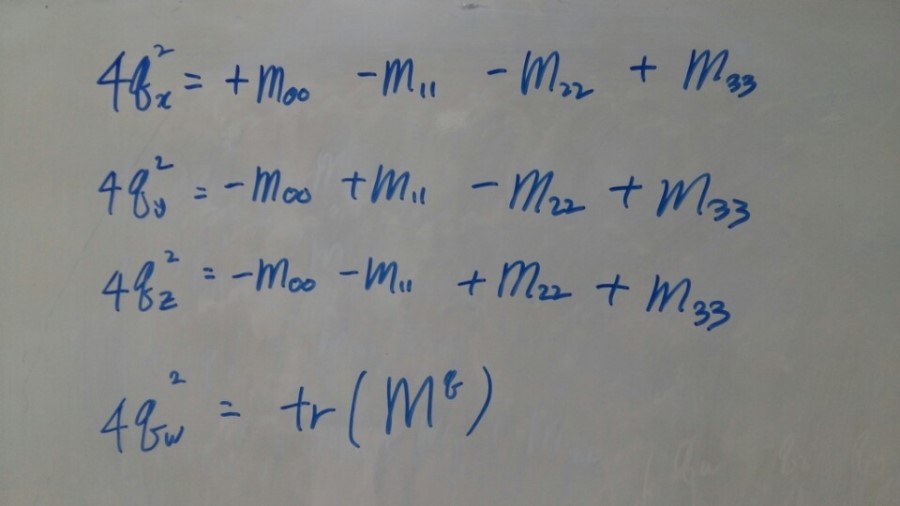
[그림9]
끝!