The Geometry of linear algebra

Linear Algebra!

This is to solve linear equations. In this post, I’m going to explain what is the geometry of linear equation.

Let’s take an example of linear equations.

2x - y = 0
-x + 2y = 3

What is the matrix of this? A Matrix is just a rectangular array of numbers

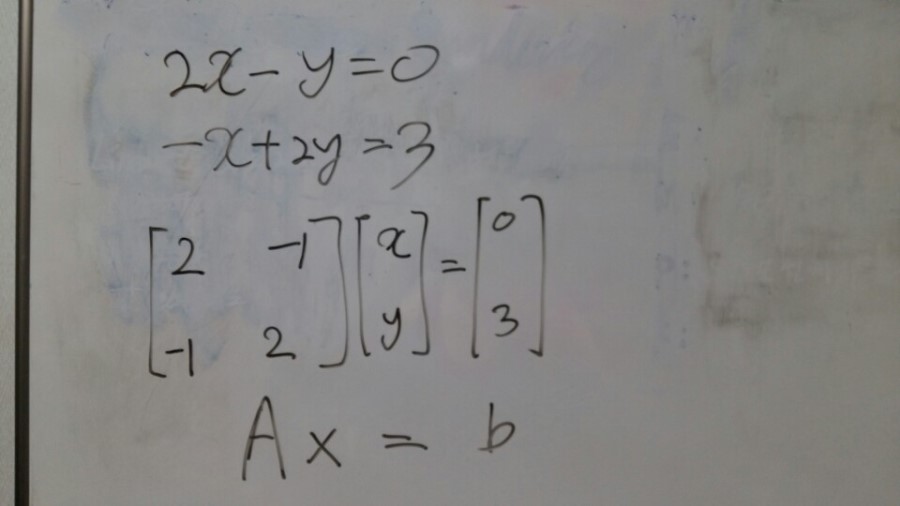
[pic1]

I can draw the matrix like this.
The left side are just numbers, Row 1 are 2 and -1. And row 2 is -1 and 2.
Then, What is the right?
Right is just unknown numbers. We’ve got two unknown, X and Y.

And We’ve got two right hand side that goes into a vector 0 3.
I will think of this as Ax = b.
A is a matrix, The matrix of coefficient.
X is a vector of unknown x y.

I can draw this equation like this.

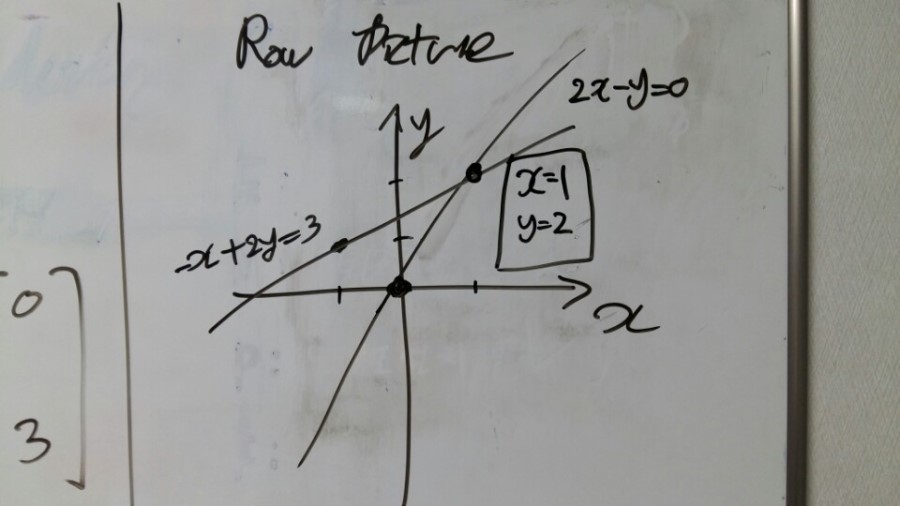
[pic2]

This is the row picture. We’ve already known about this.

Now let’s get back to the linear equation.

2x - y = 0
-x + 2y = 3

Here’s the column 1 and column 2 of the matrix.
And by multiplying some numbers, we will get the 0 and the 3. Now What is the equation, asking for?
Column 1 and column 2 is a vector.
By multiplying some numbers, we can get the right-hand side numbers.
It’s just a linear combination of columns.

[pic3]

And it’s the most fundamental operation.
Okay. Now what’s the picture of this operation? As geometry side.

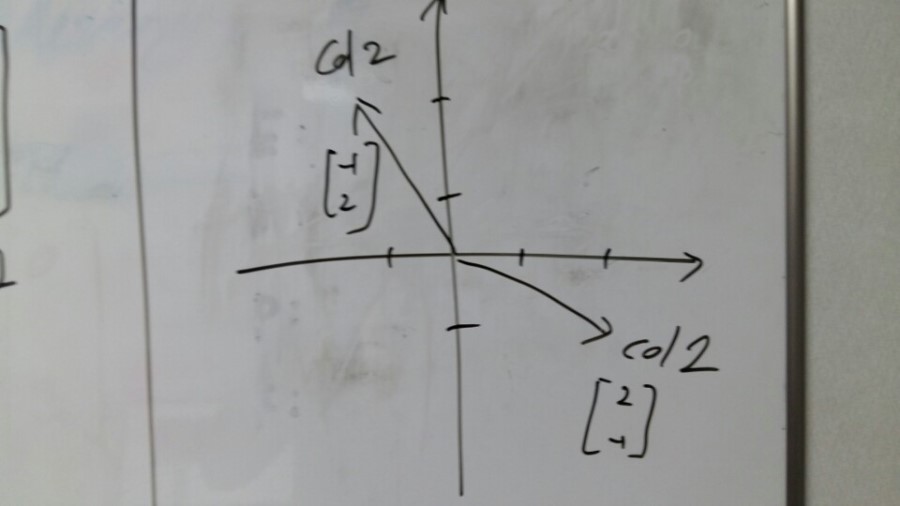
[pic4]

Here’s just two vectors. Column 1 and column 2.
And here’s the numbers(1,2) for x, y which we’ve already got in the picture 2.
Let’s just multiply the answer to the columns.

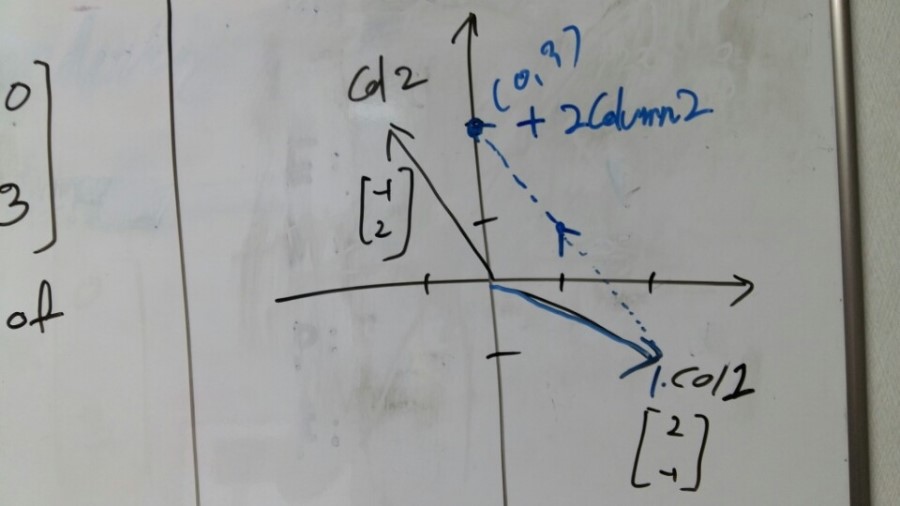
[pic5]

As a result of vector add operation, we’ve got the new vector 0, 3.

New Let’s see the result of 3-dimension equations.

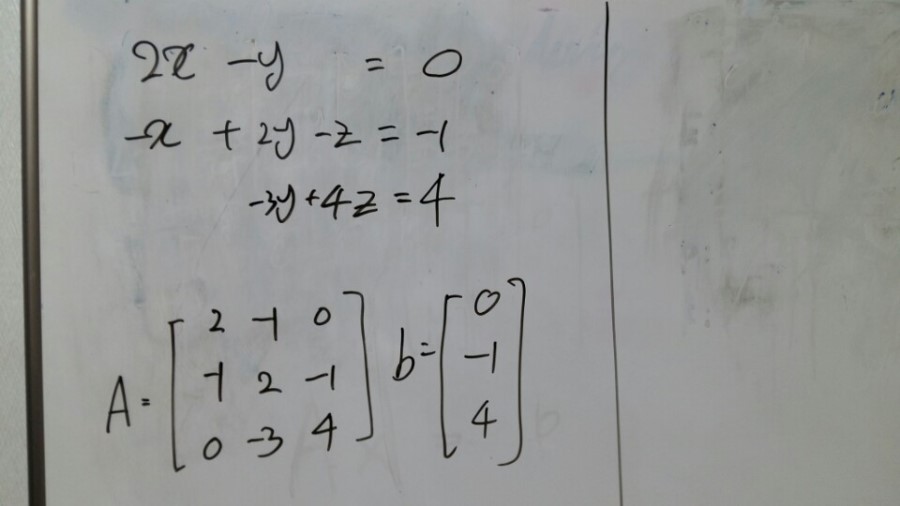
[pic6]

If I draw this equations, It would be like this. (Not exactly, but anyway each plane will contain the points. And there would be some point each point of plane is met. If there exists the answer.)

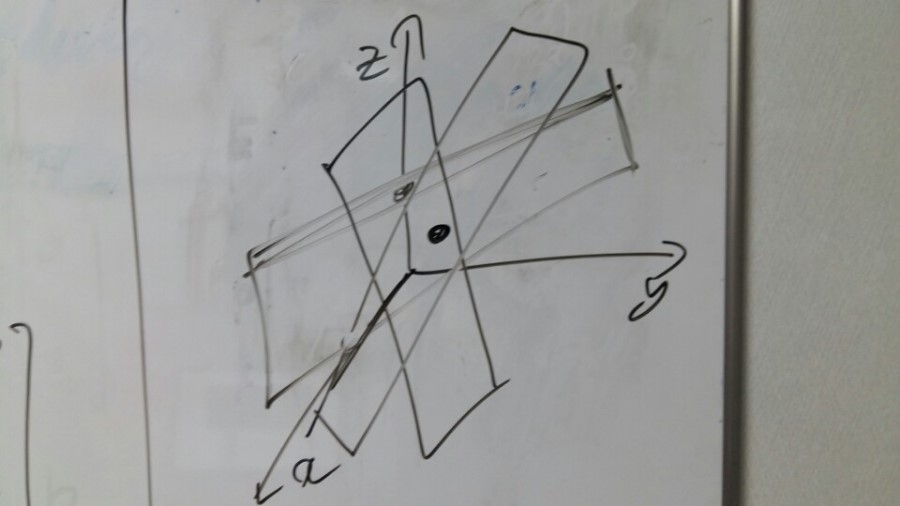
[pic7]

Now let’s see the combination of columns, which I’ve mentioned before.

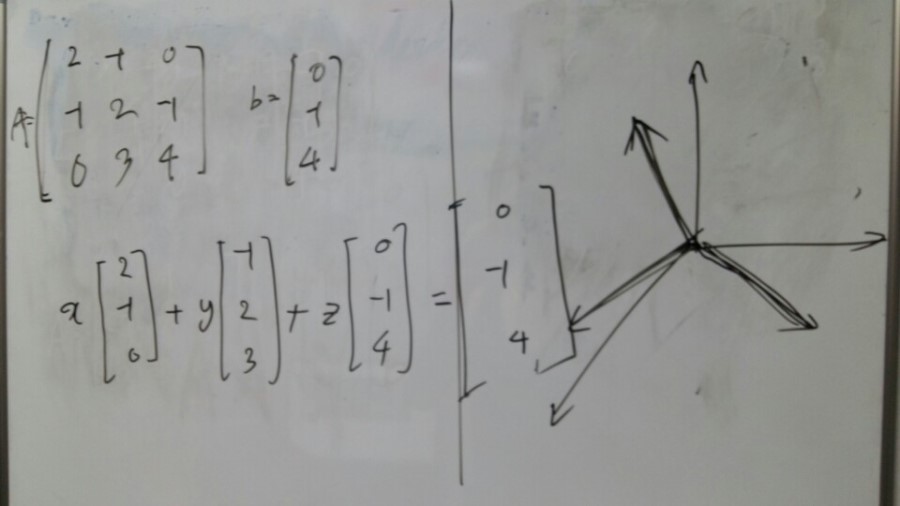
[pic8]

We would get the answer of b(0 -1 4 ) from the column combinations. In this case, x =0, y =0, z=1.
Then here’s the question. Can we get the answer for every b?
Other words, Do the linear combination of columns fill 3d space?

The Answer is yes. At least for this matrix. For these columns.
Then when could it go wrong?
If all of these columns are on the same plane?
Then we are in trouble.

Now let’s just conclude.
In summary, What is the multiply a matrix and a vector in Ax = b?
It’s a combination of columns!

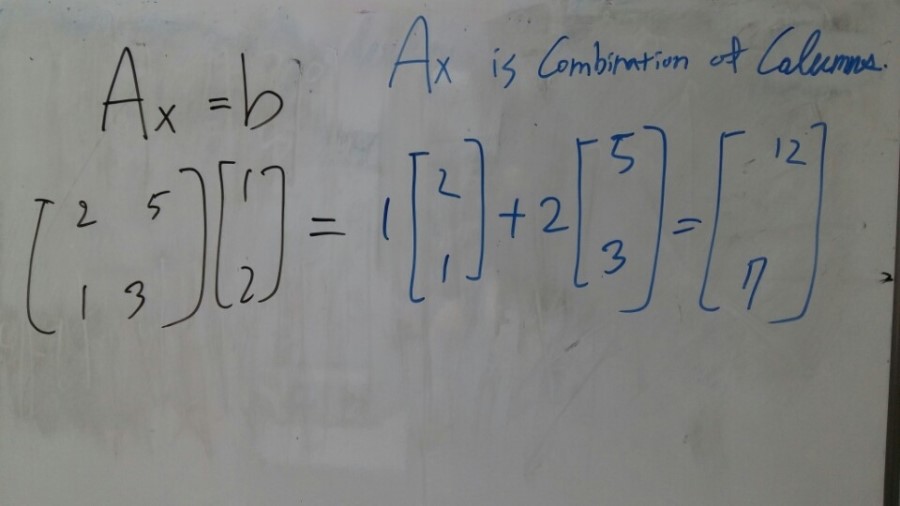
[pic9]

Reference: https://www.youtube.com/watch?v=ZK3O402wf1c&list=PLE7DDD91010BC51F8